Block-Coordinate Frank-Wolfe for Structured SVMs

The structured support vector machine (SVM) is a popular approach to learn the parameters of a structured output model. While various minimization procedures exist to solve the resulting optimization problem, in practice these solvers converge rather slowly. Our recent work at ICML 2013 (joint with Simon Lacoste-Julien, Martin Jaggi and Mark Schmidt) introduces a novel online learning algorithm, the block-coordinate Frank-Wolfe (BCFW) algorithm. It has favorable convergence rates, both in theory and practice. This blog post highlights a few key points of the BCFW algorithm and gives pointers on how to use the Matlab source code in your own project.

Our Contributions #

Our paper demonstrates how the standard batch Frank-Wolfe algorithm (also check Martin’s ICML 2013 paper) can be applied to the dual of the structured SVM. The resulting algorithm is closely related to the cutting plane algorithm, which is used in SVMstruct, a popular solver for structured SVMs. Unfortunately, just like SVMstruct, the convergence of the Frank-Wolfe algorithm is however still quite slow.

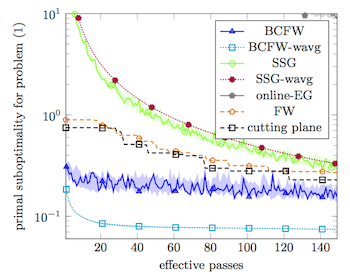
Secondly, we introduce a block-coordinate variant of the Frank-Wolfe algorithm. It is applicable to minimization problems where the domain has the form of a product domain. This is the case for the dual of the structured SVM, where the dual variables for each data point are living in a simplex. The application to the structured SVM then gives an online solver which is similar to the stochastic subgradient method (SSG): The parameters are updated after visiting a single data point, rather than the whole dataset. The key advantages of BCFW over SSG are the fact that one can perform an analytic line-search to optimize the step size, as well as track the primal-dual gap. In the experiments we studied this resulted in substantially improved convergence speed.

Finally, we observe even better convergence by building a weighted average of the iterates. This is in line with recent work (see Lacoste-Julien et al and Shamir and Zhang).

The Matlab Sources #

We just released a Matlab source code that demonstrates the usage of BCFW for the training of structured SVMs. You can find the sources on github. The demo implements optical character recognition on the dataset by Ben Taskar. The sources also include two alternative solvers: the standard Frank-Wolfe algorithm (which is very similar to the cutting plane algorithm used in SVMstruct) and the stochastic subgradient method (a.k.a. Pegasos or stochastic gradient descent).

You should be able to use the BCFW script in your own problems quite easily. You only need to define three functions: the joint feature map, the maximization oracle and the loss function. For an example of how do this, check the files chain_featuremap.m, chain_oracle.m and chain_loss.m in the demo/chain folder.